科学计算器使用教程 科学计算器
![]() admin2023-03-20【电脑技术】浏览:186
admin2023-03-20【电脑技术】浏览:186
科学运算问题是科学与工程中的重要问题。在当前一般高校理工科课程设置中,高等数学、线性代数、概率论与数理统计等为必修课程,有些专业还有复变函数、积分变换、最优化、数值分析等选修课程。有了这些数学基础,很多专业课程相应的数学模型就可以建立起来,而这些数学问题的求解就成了不容回避的问题。因此,利用工具求解科学运算问题。在科学研究与工程实践中都是特别重要的。
子曰“工欲善其事,必先利其器”,MATLAB语言是高效求解科学运算问题的利器。
MATLAB语言是学术界与很多工程领域使用广泛的专业计算机语言。对理工科学生而言,尽早学习、掌握这样的主流计算机语言,才能有机会提早在课程学习与课外活动中使用MATLAB语言,更好地解决学习、实践中遇到的问题。例如,在传统课程的学习中,至少可以从一个新的视角审视学习的内容,探讨利用计算机解决实际问题的方法,甚至创造性地解决前人没有解决的问题。
在总结多年实际教学经验的基础上,薛定宇教授曾在首届MathWorks亚洲研究教育峰会(2014年11月,东京)上提出了科学运算问题的“三步求解方法”。这三个步骤分别为“是什么”“如何描述”和“求解”。在“是什么”步骤中,侧重于数学问题的物理解释和含义。即使使用者没有学习过相关的数学分支,也可能通过简单的语言叙述大致理解问题的物理含义。在“如何描述”步骤中,用户应该知道如何将数学问题用MATLAB描述出来。在“求解”步骤中,用户应该知道调用哪个MATLAB函数将原始数学问题直接求解出来。如果有现成的MATLAB函数,则应该调用相应函数直接求解出问题;如果没有现成函数,则编写出通用程序得出问题的解。
有了这样的思路,普通研究者就可以直接利用计算机工具在短时间内解决已经学习过甚至从未接触过的科学运算问题。本书涉及大量科学运算问题的求解实例,基本采用的就是这样的“三步求解方法”。
下面通过两个实例演示“三步求解方法”。
实例1
例 用三步求解方法求解下面的线性规划问题。
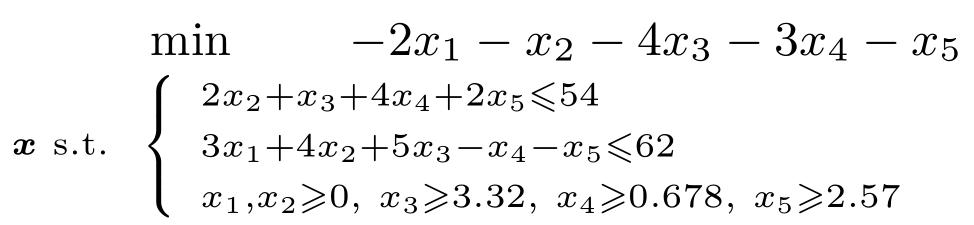
解 有的读者很可能没有系统地学习过最优化等相关的课程。不过不要紧,即使没有学习过相关的理论知识,也可以通过下面的三步求解方法得出问题的解。
(1)“是什么”。
本步先理解每个数学问题的物理含义。在这个具体问题中,读者可以将原始问题从字面上理解为:在满足联立不等式约束
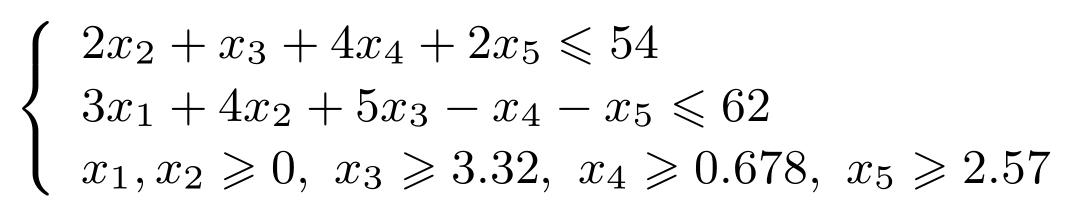
的前提下,怎么发现一组决策变量xi的值,使得目标函数
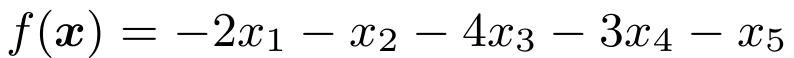
的值为最小。所以,即使没有学习过最优化课程的读者也不难从字面上理解该问题的数学公式。
(2)“如何描述”。
读者将学会如何将数学问题用MATLAB函数描述出来,通过几分钟线性规划问题求解的学习,就可以用下面的方法建立一个变量 P 描述整个数学问题:
>> clear; P.f=[-2 -1 -4 -3 -1]; % 目标函数P.Aineq=[0 2 1 4 2; 3 4 5 -1 -1]; P.Bineq=[54 62]; % 约束条件P.solver='linprog'; P.lb=[0;0;3.32;0.678;2.57]; % 下边界P.options=optimset; % 将整个线性规划问题用结构体变量P描述出来(3)“求解”。
调用线性规划求解函数 linprog() 直接求解问题,得出问题的解为 x1 = 19.785,x2 = 0,x3 = 3.32,x4 = 11.385,x5 = 2.57。
>> x=linprog(P) % 调用 linprog() 函数求解数学问题实例2
例 人工神经网络是近年来应用较广泛的智能类数学工具,擅长于数据拟合与模式分类等运算。假设由下面的语句生成样本点数据:
>> x=0:0.1:pi; y=exp(-x).*sin(2*x 2);试利用样本点建立人工神经网络模型,并绘制函数曲线。
解 如果不想花时间或没有时间学习人工神经网络的系统理论,只想使用神经网络解决本例的数据拟合问题,则可以考虑利用前面介绍的三步求解方法,花几分钟了解神经网络基本概念与使用方法,就能利用人工神经网络求解数据拟合问题。回到前面提及的三步求解方法。
(1)什么是人工神经网络。
其实没有必要去了解人工神经网络的技术细节,只须将人工神经网络看作一个带有可调参数的信息处理单元,它接受若干路信号进行处理,得出输出信号。
(2)如何将神经网络的数学模型建立起来。
选择 fitnet() 函数建立带有 5 个节点的空白神经网络模型,用 train() 训练神经网络,调节神经网络的内部参数,更好地适应样本点。由下面的命令就可以得出所需的人工神经网络模型,如图 1-1 所示。
>>net=fitnet(5);net=train(net,x,y),view(net)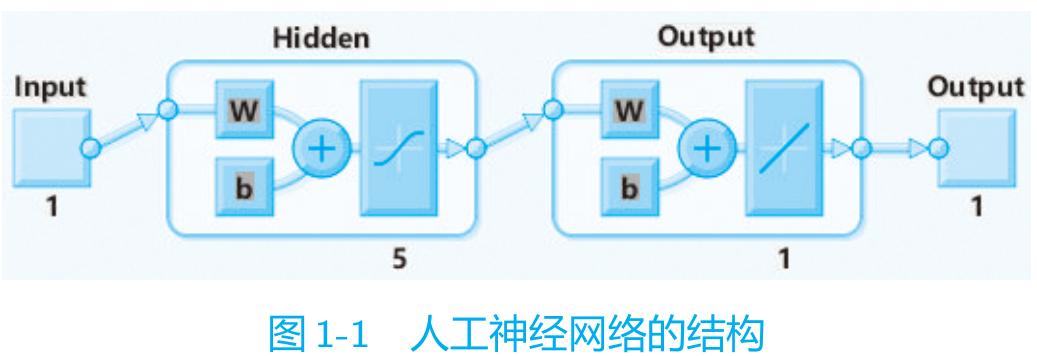
(3)求解曲线拟合问题。
使用神经网络绘制曲线,并与理论值比较,如图 1-2 所示。可见,即使不系统学习人工神经网络,也可以直接利用人工神经网络解决实际问题。用户还可以调整神经网络的结构参数,如修改节点个数等,通过实践观察和比较不同参数下曲线拟合的效果。
>> t0=0:0.01:pi; y1=net(t0); y0=exp(-t0).*sin(2*t0 2);plot(t0,y0,t0,y1,'--',x,y,'o') % 比较理论值与拟合结果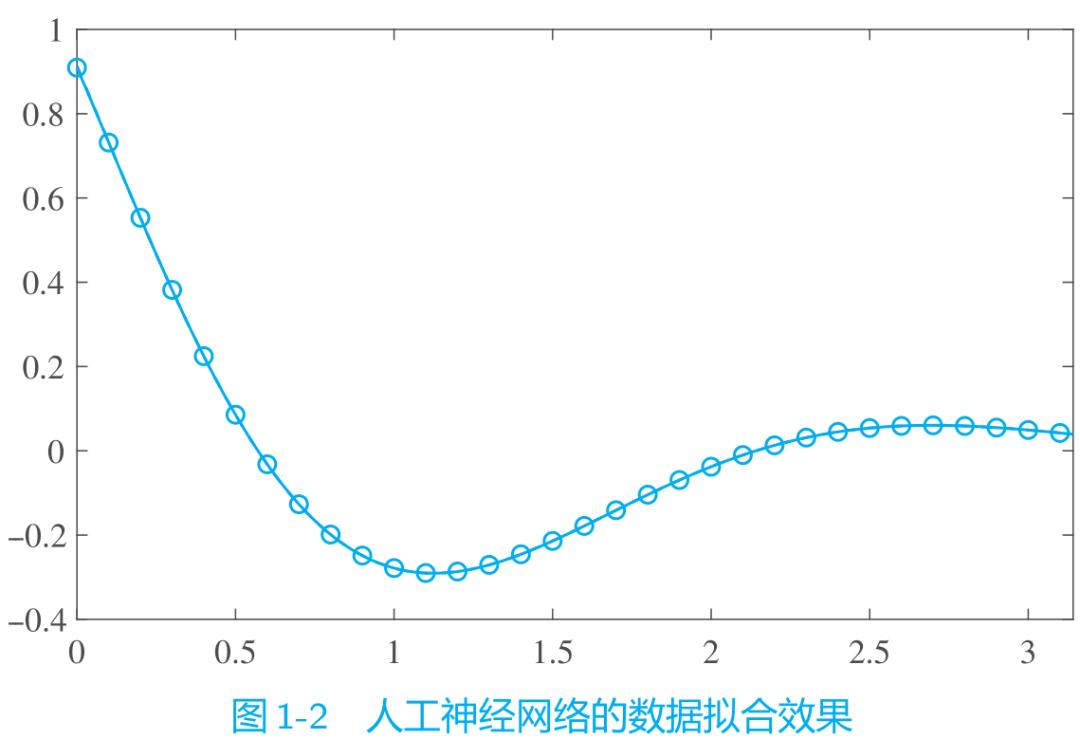

热评文章
企业微信分屏老师能看到吗 企业微信切屏老师能看见吗
excel如何批量输入求和公式 excel批量输入求
罗技驱动win7能用吗 罗技鼠标支持win7系统吗
打印机驱动卸载干净教程 打印机驱动怎样卸载干净
显卡驱动更新小技巧,让你的电脑运行更稳定
手机系统声音不起眼,但很重要 手机系统声音有的,但